Advanced Logic
Table of Contents
Intro to Modal Logic (operators, frames, models, tautologies)
First-order propositional logic
Includes variables, T, ⊥, not, and, or, implication. Proofs are given by structural induction. Precedence is ¬, then ∧∨, then →.
a valuation v : Var → {0,1} maps propositional variables to truth values. i.e., it tells you what variables are true.
the semantics of a formula under a valuation is defined with ⟦p⟧ᵥ = v(p), with p ∈ Var
if ⟦φ⟧ᵥ = 1 (i.e. φ is true in v), we write v ⊨ φ (read “v models φ”).
- then also: φ has a model, namely the model with state v, so φ is satisfiable
If every model of all φᵢ is a model of ψ, we write φ₁,…,φn ⊨ ψ
- then ψ is a semantic consequence of φ₁,…,φn
If v ⊨ φ for all valuations of v, then universally ⊨ φ (φ is a tautology)
Soundness: ⊢ implies ⊨ (“what we can derive is true”). proved by induction on length of proof
Completeness: ⊨ implies ⊢ (“what is true can be derived”). can be proven using consistency
Basic modal logic
Basic model logic operators:
- □: necessary, known, provable
- ◇: possible, considered possible
In a diagram, one of these symbols is exactly one transition step (use multiple for multiple steps).
- ◇ φ ⇔ ¬□ ¬φ
- □ φ ⇔ ¬◇ ¬φ
Examples in natural language:
- “whatever is necessary is possible” == □φ → ◇φ
- □ can also mean “I know”, e.g. “I know that someone appreciates me” == ∃x.□A(x, M)
Loeb’s formula: □ (□ p → p) → □ p
Veridicality: □ φ → φ
Truth is relative to current situation/world/environment:
- formulas evaluated in given structure (i.e. world, model, frame, or universally)
- necessity (□): truth in all accessible worlds. if there are no accessible worlds, it’s true.
- □ T: holds always
- □ ⊥: holds in blind states (those without a successor)
- possibility (◇): truth in some accessible world (at least one). if there are no accessible worlds, it’s false.
- ◇ ⊥: never holds (can never do a step to a state where ⊥ holds)
- ◇ T: holds in states with a successor
Dualities:
- ◇ φ ≡ ¬ □ ¬ φ
- □ φ ≡ ¬ ◇ ¬ φ
Frames
A situation is set by a frame F = (W,R)
- W ≠ ∅ set of possible worlds/states
- R ⊆ W × W an accessibility/transition relation
A frame is just the states and transitions between them, without a valuation (i.e. without saying what’s true in each state).
A frame could be (ℕ, <), or ({1,2,3,4}, {(1,2), (2,4), (1,3), (3,4), (2,2)})
Models
model: pair M = (F, V)
- a frame F = (W,R)
- a valuation V : Var → W → {0,1}, or V : Var → P(W)
- the valuation says which letters/formulas are true in which states
- possible notation:
- V : Var → P(W) means Var → W → {0,1}
- V(p,w) = 1 is the same as w ∈ V(p)
pointed model: pair (M,w) of model M and w a world in M (i.e. you zoom in to a specific state in M)
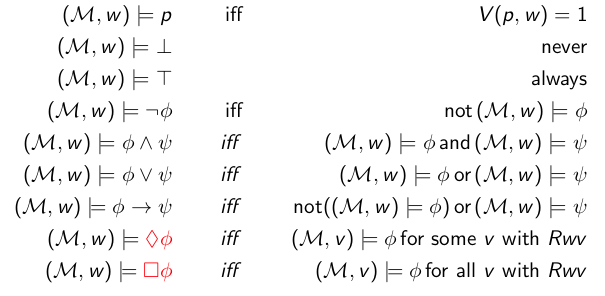
Distinguishing and characterizing states
A formula φ characterizes a state x in model M if φ is true in x but not in other states of M.
A formula φ distinguishes state x from state y in a model M if φ is true in x but not in y.
Example
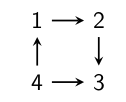
Above:
- the formula 3 ⊨ □ ⊥ characterizes state 3
- the formula 2 ⊨ ◇ □ ⊥ characterizes state 2