Propositional dynamic logic (PDL)

In propositional dynamic logic (PDL), aim to prove: φ → [while σ do α] ψ

i.e. starting with φ true, for any terminating execution of the program, we have ψ true.

Definitions:

state of program execution: state/world
program: regular program which slightly generalizes a while program
statement {pre}program{post}: formula pre → [program] post

For every program α we have modality 〈α〉:

〈α〉φ: it’s possible to execute α from current state, and successfully halt in state satisfying φ (like existential quantification)
[α]φ: for all executions of α, if α successfully halts, then it halts in a state satisfying φ (like universal quantification)

Program definitions:

a: program from set A of atomic programs (letters, like in prop. logic)
α; β: sequential composition
α ∪ β: non-deterministic choice
α*: iteration, 0 or more times.
φ?: test, depends on the grammar for formulas
- if φ then continue without changing state, if not then block without halting

Examples of formulas:

Formula examples

We obtain semantics of PDL as instance of multi-modal logic.

Operators:

composition “R;S” = {(x, z) | ∃ y : Rxy ∧ Syz}
union “R ∪ S” = {(x, y) | Rxy ∨ Sxy}
R*: repeat R one or more times

A model M is a PDL-model if the frame is a PDL-frame and $R_{\phi ?} = \{ (w,w) \;|\; M, w \models \phi\}$

The R of the frame is all sets of Rₐ where a is a program (i.e. a label on an arrow).

Proof example of 〈α, β〉 p → 〈α〉〈β〉p

Take a PDL model and a state x.
Assume x ⊨ 〈α, β〉 p
That is, there is a state y such that $(x, y) \in R_{\alpha;\beta}$ and y ⊨ p.
$R_{\alpha;\beta} = R_{\alpha}; R_{\beta}$
That is, there is a state u such that $(x, u) \in R_{\alpha}$ and $(u,y) \in R_{\beta}$.
Because $(u,y) ∈ R_{\beta}$ and y ⊨ p, we have u ⊨ 〈β〉 p
Because $(x,u) ∈ R_{\alpha}$, we have and u ⊨ 〈β〉p we have x ⊨ 〈α〉〈β〉p.

If then else:

program: if p then a else b
encoding: (p?; a) ∪ (¬ p? ; b)

Example

Model

Graphviz code

digraph g {
rankdir=LR
1 [xlabel="[p]"]
1 -> 2 [label="a"]
4 -> 2 [label="b"]
1 -> 3 [label="b"]
4 -> 3 [label="a"]
}

Calculate the relation for if p then a else b, which is encoded as (p?; a) ∪ (¬ p?; b):

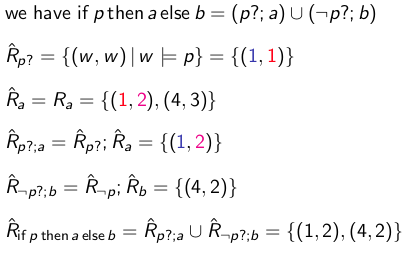
Calculation

While:

program: while p do a
encoding: (p?; a)*; ¬ p?

Example

Model

Graphviz code

digraph g {
rankdir=LR
1 -> 2 [label="a"]
2 -> 3 [label="a"]
3 -> 4 [label="a"]
4 -> 5 [label="a"]
5 -> 6 [label="a"]
1 [xlabel="[p]"]
2 [xlabel="[p]"]
3 [xlabel="[p]"]
4 [xlabel="[p]"]
}

Calculating the relation while p do a, encoded as (p?; a)*; ¬ p?:

Calculation

If E is a bisimulation between two A-models, then it is a bisimulation for the models’ PDL-extensions. However, intersection and inverse are not safe for bisimulation.

Advanced Logic

Table of Contents

Propositional dynamic logic (PDL)