Standard translation: mapping basic modal logic to first-order predicate logic

Aim to map formulas of basic modal logic to first-order predicate logic such that:

• φ in BML is valid iff its translation in first-order predicate logic is valid
• φ in BML is satisfiable iff its translation in first-order predicate logic is satisfiable

Translation:

• translate “p is true in world x” as “predicate P holds for x”
• translate “accessibility relation R” as “binary predicate R”
• translation is relative to some state
• notation: Px instead of P(x), Rxy instead of R(x,y)

Rules for standard translation:

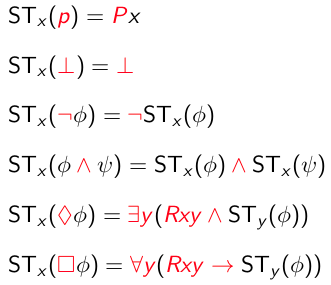
Examples of translation:

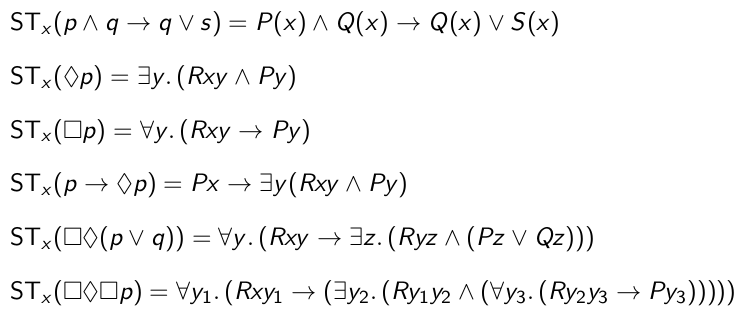
first-order predicate logic is decidable if it uses at most 2 variables. therefore, adapt standard translation to only use 2 variables.

In a formula, check the situation with bound variables, and rename where possible. When you are in state a and start a quantification, use the variable b, and vice versa.