Temporal logic using temporal frames

Linear time logic: events along a single computation path. ‘at some point we will have p’

Branching time logic: quantify over possible paths. ‘there is a path where eventually p’

A frame F = (T, <) is a temporal frame if both:

• < is irreflexive: not t < t for all t
• < is transitive: if t < u and u < v then t < v

Truth and validity:

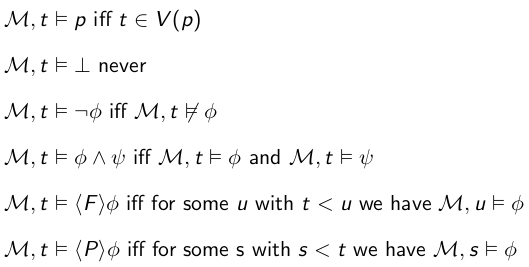
Right-linearity:

• “all future points are related”
• definition: ∀ x,y,z: (x < y) ∧ (x < z) → (y < z) ∨ (y = z) ∨ (z < y)
• is modally definable

Right-branching:

• “right-branching is not right-linear, so some point has two unrelated points in the future”
• definition: there exist x,y,z such that x < y and x < z but ¬ (y < z) ∧ y ≠ z ∧ ¬ (z < y)
• is not modally definable

Discrete:

• “every point with a successor has an immediate successor
• definition: (x < y ) → ∃ z : x < z ∧ ¬ ∃ u: ( x < u) ∧ (u < z)
• is modally definable in basic temporal logic

Dense:

• “between any two points is a third one”
• definition: x < z → ∃ y (x < y ∧ y < z)
• is modally definable

Operator next:

• symbol ⊗
• M,t ⊨ ⊗ φ iff ∃ v : t < v ∧ (¬ ∃ u : t < u < v) ∧ M,v ⊨ φ
  • e.g. x ⊨ ⊗p: there a future we can reach only in 1 step from x where p holds
  • not true if other options. e.g. you can go directly from Centraal to Utrecht, but Amstel station is still there.
• next not definable in basic modal logic

Operator until:

• symbol U
• M,t ⊨ φ U ψ iff ∃ v : t < v ∧ M,v ⊨ ψ ∧ ∀ u : t < u < v → M,u ⊨ φ
  • if we have a future where ψ holds, then φ holds in all points between now and that future
• not definable in basic modal logic

Examples of until:

digraph g {
rankdir=BT
a -> b
a -> c
c -> d
b -> d
c -> e
c [xlabel="p"]
d [xlabel="q"]
e [xlabel="q"]
}

digraph g {
rankdir=BT
a -> b
a -> c
c -> d
b -> d
d [xlabel="q"]
c [xlabel="p"]
}

In a temporal frame:

• ◇ p is equivalent to T U p
• ⊗ p i equivalent to ⊥ U p