Time complexity contd.

Bounded tiling problem

Input is natural number n, finite collection of types of tiles, the first row of n tiles is it possible to tile an n × n field with the given first row? when connecting tiles, the touching side must have the same color, tiles must not be rotated.

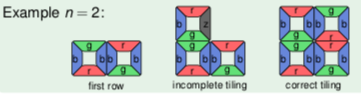
the problem is NP-complete

co-NP

Problem L is in co-NP if complement $\bar{L}$ is in NP. i.e. set of instances without solution is in NP.

we don’t know if NP = co-NP in general. but if an NP-complete problem is in co-NP, then NP = co-NP.

EXP and NEXP

Nondeterministic TM is exponential time if it runs in time $2^{p(|x|)}$ for some polynomial p.

NEXP is nondeterministic exponential, EXP is deterministic exponential.

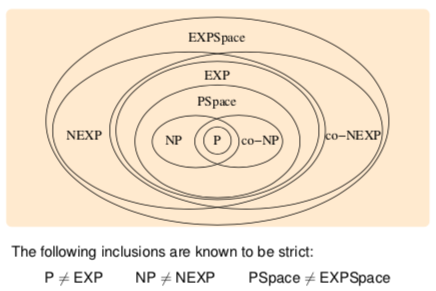
P ⊆ NP ⊆ PSpace ⊆ EXP ⊆ NEXP. we don’t know if this is strict. we know that P ≠ EXP, NP ≠ NEXP.

Space complexity

Nondeterministic Turing machine M runs in space f if for every input w, every computation of the machine visits at most f(|w|) positions on the tape. i.e. the function f is the upper bound on number of visited cells on tape (length of input word)

PSpace and NPSpace

Nondeterministic Turing machine is in polynomial space if it runs in space p for some polynomial p.

NPSpace is if it runs in nondeterministic polynomial space, PSpace if deterministic.

Savitch’s theorem: if language accepted by nondeterministic TM in f(n) space, then accepted by deterministic TM in f(n)² space. PSpace = NPSpace.

A language L ∈ PSpace is PSPace-complete if every language L’ ∈ PSpace is polynomial-time reducible to L.

Complexity hierarchy