Automata & Complexity

Grammars (contd)

Right linear grammars (contd)

1. Strict right linear grammars

   Let G be right linear grammar G = (V, T, S, P) There is a strictly right linear grammar H such that L(G) = L(H):

   1. Assume we have production rule γ of form A → u(B) with A,B ∈ V and u ∈ T^* with |u| > 1. Then u = aw for some a ∈ T and w ∈ T^+.

   2. Let X be a fresh variable, add X to V and split rule γ into:

      • A → aX
      • X → w(B)

      Then A → aX → aw(B) = u(B). So L(G) = L(H).

   3. Repeat splitting until |u|  ≤ 1 for all rules.

2. Prove right linear grammars ⇔ regular languages

   Thm: language L is regular ⇔ there is right linear grammar G with L(G) = L

   Proof ⇒:

   • translate NFA/DFAs into right linear grammars: use states as nonterminals and transitions as rules

   Proof ⇐:

   • build NFA from right linear grammar

Left linear grammars

Left linear: all production rules only have non-terminals on left side

Thm: language L is regular iff there is left linear grammar G with L(G) = L.

Proof: L regular ⇔ L^R is regular ⇔ right linear grammar for L^R ⇔ left linear grammar for L (reverse all production rules)

Mixing right and left linear rules doesn’t mean that the generated language will be regular!

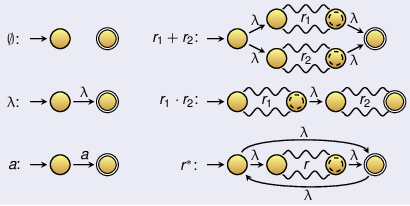
Regular expressions

Definition of regex over alphabet Σ:

• ∅, λ are regular expressions
• a is regular expression for ever a ∈ Σ
• r₁ + r₂ is regular expression for all regexes r₁ and r₂
• $r_1 \cdot r_2$ is regex for all regexes r₁ and r₂
• r^* is regex for all regexes r

Regex to NFA

For every regex r, build NFA such that:

• L(M) = L(r)
• M has precisely one final state (different from the starting state)

NFA to regex

1. Transform M st there is only one final state. If M has multiple final states:

   • add fresh state q_f to M
   • for every final state q in M, add arrow $q \xrightarrow{\lambda} q_f$ to M
   • define q_f as only final state

2. Remove all double arrows. Use transition graphs with regexes as labels. If there are e2 arrows from state q₁ to q₂ with labels r₁ and r₂, replace them by one arrow with label r₁ + r₂. It might be that q₁ == q₂, then arrows are loops.

   

3. As long as there are states other than starting and final state:

   • remove one state q

   • for all states q₁,q₂ and arrows $q_1 \xrightarrow{r_1} q$ and $q \xrightarrow{r_2} q_2$, add arrow from q₁ to q₂ as follows:

     • if arrow $q \xrightarrow{r} q$:

       

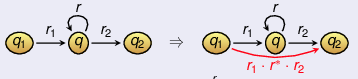
     • otherwise:

       

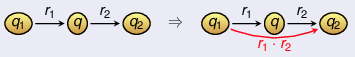
4. If F  ≠ q₀, then transition graph is reduced:

   

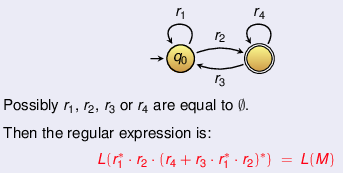
Alternative descriptions of regular languages

These statements mean the same thing:

• there is DFA M with L(M) = L
• there is NFA M with L(M) = L
• there is right linear grammar G with L(G) = L
• there is left linear grammar G with L(G) = L
• there is regular expression r with L(r) = L