*[TM]: Turing Machine *[BFS]: breadth-first search

Variations of Turing machines

With multiple tapes

A TM with two tapes can be simulated by a TM with one tape: transition on two tapes translates to multiple transitions on one tape. The difference in time complexity between TM with one tape and multiple tapes is a polynomial factor.

Nondeterministic Turing machines

Nondeterministic TM has transition function $\delta : Q \times \Gamma \rightarrow 2^{Q \times \Gamma \times \lbrace L, R \rbrace}$

A nondeterministic TM can be simulated by a deterministic TM:

• the deterministic TM can use breadth-first search to simulate all executions of nondeterministic TM in parallel.
• the branches of the BFS can be stored on tape in form of queue

Difference in time complexity between deterministic and nondeterministic TM is exponential factor

Universal Turing machines

A TM is “universal” if it can simulate every TM.

A universal TM gets as input: Turing machine M (described as word w), input word u. It simulates M on u. The inputs can be written on two different tapes, or behind each other on one tape.

The theorem is that there is a Turing machine. You just gotta believe it.

Unrestricted grammars

These correspond to Turing machines.

Unrestricted grammar contains rules x → y, where x ≠ λ (and that’s the only constraint).

Language L is generated by unrestricted grammar ↔ L is accepted by a Turing machine.

Unrestricted grammars → Turing machines

For every unrestricted grammar there is Turing machine st the languages generated/accepted are identical.

How do you do it?

• input for machine M is word w, written on tape
• M can do BFS for derivation of w from S.
• if derivation found, then w accepted by M.
• then the two languages accepted/generated are equal.

Turing machines → unrestricted grammars

For every Turing machine M there is an unrestricted grammar st the languages generated/accepted are identical.

How do you do it?

• Sorry, the stuff he put in the slides is too abstract for me here. When I actually have to learn it, I’ll try to write it in a way that’s easier to understand.

Context-sensitive grammars

Context-sensitive grammars

Grammar is context-sensitive if, for every rule x → y, |x| ≤ |y| and x ≠ λ.

For every context-sensitive grammar, there is a grammar that generates the same language, with rules of the form xAy → xvy (with v ≠ λ).

A language is context-sensitive if there is a context-sensitive grammar for it.

Linear bounded automata

A nondeterministic TM (Q, Σ, Γ, δ, q₀, F).

There is no □; instead, symbols [ and ] are placed around the input word.

For every state q:

• δ(q,[) is of the form (q’,[,R)
• δ(q,]) is of the form (q’,],L)

The memory is restricted by the length of the input word.

A language accepted by a linear bounded automaton is a word reached from the start state, of the form [uqv], where q is a final state and u,v ∈ Γ*.

Context-sensitive grammars to LBAs

For every context-sensitive grammar, there is an LBA that generates the same language.

A derivation of a word in the language contains only words of same or smaller length. A nondeterministic Turing machine can simulate (guess) this derivation without leaving the bounds of w.

LBAs to context-sensitive grammars

For every LBA, its language is context-sensitive.

Build unrestricted grammar of the same language; then, all production rules are context-sensitive except for □ → λ. However, LBA does not use □, since it never leaves borders of input word. So, drop rule □ → λ, and rules including □.

Basic properties of context-sensitive languages

If $L_1$ and $L_2$ are context-sensitive, then so are $L_1 \cup L_2$, $L_1 \cap L_2$, $L_{1}^{{R}$, $L_{1}L_{2}$, $L_{1}}{*}$, $\overline{L_1}$, $L_{1} \setminus L_2$

Proofs:

• $L_1 \cup L_2$, $L_{1}^{{R}$, $L_1 L_2$, $L_{1}}{*}$: using grammars/automata
• $L_1 \cap L_2$: using LBAs
• $L_1 \setminus L_2 = L_1 \cap \overline{L_2}$
• $\overline{L_1}$: proven by people smarter than us (Immerman, Szelepcsenyi)

We don’t know if deterministic LBAs are as expressive as nondeterministic LBAs.

Recursively enumerable languages

Language is recursively enumerable if it’s accepted by a Turing machine.

Turing machines are recursively enumerable:

• a TM can be represented as a word
• a parser can check whether a word represents a TM, and if so, accept
• so, there is recursive enumeration of all TMs

Properties of recursively enumerable languages

The class of recursively enumerable Languages is closed under ∪ and ∩. There exist recursively enumerable languages for which their complement is not recursively enumerable.

Recursive languages

A language is recursive if it, and its complement, is recursively enumerable. Not every recursively enumerable language is recursive.

Language is recursive ↔ it is accepted by a deterministic TM that halts for every input.

Context-sensitive languages are recursive, but not every recursive language is context-sensitive.

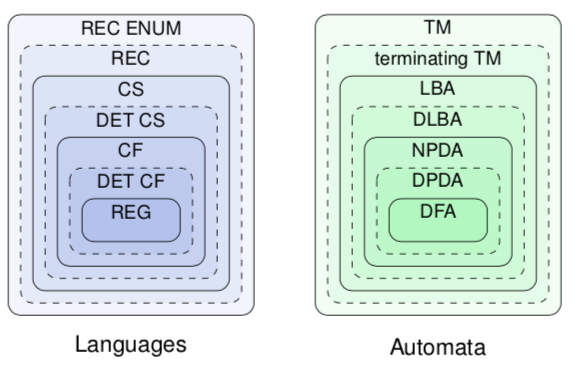
The Chomsky hierarchy

Countability

Turing machines are countable, languages aren’t.

There are countably many Turing machines over an input alphabet Σ. There are uncountably many languages over Σ.

Why:

• let a be a letter in Σ
• assume L₀, L₁,… is enumeration of all languages over {a}
• define language L as follows: for every i ≥ 0, $a^{{i} \in L \Leftrightarrow a}{i} \notin L_i$
• then for every i ≥ 0, $L \neq L_i$
• then L is not part of the above enumeration; contradiction.
• so, not all languages are recursively enumerable