Computer Networks
Table of Contents
Data Link: Error detection/correction
Errors
- errors can be caused by hardware or software
- timer that expires if frame not acknowledged, then frame is resent
- flow control is feedback-based (receiver sends permission to sender for more data), or rate-based (built-in data send rate limiter)
Error detection
- adds enough redundancy so that receiver can detect error and request retransmission, used on highly reliable networks like fiber
- a codeword is n-bit unit with m data bits and r check bits
- parity bit
- add a single bit to the end to make the number of 1s even
- a code with a single parity bit can detect single-bit errors
- however, not good with burst errors
- to improve, interleave — compute parity in order different from transmission order:

- checksums
- 16-bit Internet checksum — sum of message bits divided into 16-bit words
- Fletcher’s checksum — adds product of data and its position to running sum
- improved error detection over parity
- detects bursts up to N errors
- does not detect systematic fuckups
- Cyclic redundancy check
-
based on treating bit strings as polynomials with coefficients of only 0 and 1
-
polynomial eg. ×32 + x16 + x8+×1 + 1
-
sender and receiver agree on generator polynomial G(x) in advance, with both high- and low-order bits at 1
-
append a CRC to end of frame so that polynomial represented is divisible by G(x)
-
algorithm to send, with generator G(x):
-
r is degree of G(x) — append r zero bits to end of frame so it now has m+r bits
-
divide bit string G(x) into bit string from step 1 with long division (subtracting is mod 2, simply XOR)
-
subtract remainder from bit string in step 1 using mod 2 subtraction, result is checksummed frame to transmit
-
-
when received, checks if frame is divisible by G(x). if not, the remainder is the error (E(x)/G(x))
-
Error correction
- adds enough redundancy to be able to correct errors, used on unreliable networks like 802.11
- Hamming distance
- shortest distance to change one string into another
- compute: XOR two bit strings and count number of ones in result
- with Hamming distance d, you can detect d-1 errors
- Hamming codes (video)
-
if Hamming distance n, we can correct (h-1)/2 errors
-
bits of codeword are numbered, with 1 at very left
-
at powers of 2 are check bits, others are data
-
sender:
-
expand locations into powers of 2
-
decide Value of check bit in location 2i by mod 2 adding all bits with 2i in expansion
-
-
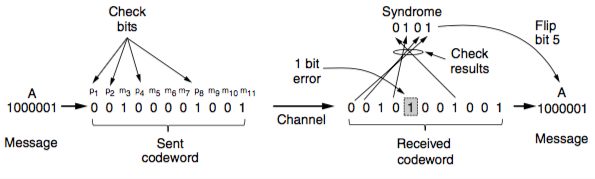
receiver:
-
Redo all bit computations
-
For even parity, each check result should be zero. If not, an error has been detected.
- check bits for whole message are error syndrome
- convert to decimal n, then nth bit is error
-
-
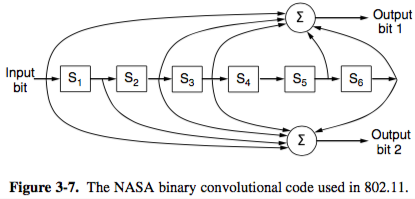
- Convolutional code
- encoder processes input bits & generates output bits
- output depend’s on current and previous input bits (constraint length)
- encoder has memory, e.g. in six registers
- e.g. NASA r=1/2 and k=7 (also in 802.11) — each input bit on left side produces two output bits that are XOR sums of input and internal state: