Graphs

What is a graph?

a set of vertices (nodes) and a set of edges (arc/arrows) connecting pairs of vertices

consists of a collection V of vertices and collection E of edges, for which we write G = (V, E)

each edge e ∈ E is said to join two vertices (end points) if e joins u, v ∈ V, we write e = (u, v)

V — finite set of vertices E — set of edges (pairs of vertices)

V = {a, b, c, d, e, f}

E = {(a,c), (a,d), (b,c), (b,f), (c,e), (d,e), (e,f)}

Types of graphs

Completeness

A graph is complete if you have n vertices and *n-1 *edges on each vertex. Must be simple and undirected.

Edges properties

• connects two vertices
• an edge connecting vertices *i *and j is written as ij
• sometimes has a direction (i —> j)
• weights assigned by means of numbers (e.g. distance between two vertices)

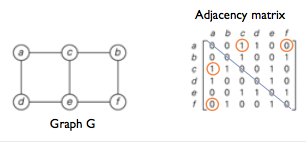
Adjacency Matrix representation

Notation: A[i,j]

Symmetric: A[i,j] = A[j,i]

when a graph is undirected, the adjacency matrix is always symmetric