Intro

Distributed vs uniprocessor

• Lack of knowledge on global state: process has no up-to-date knowledge on states of other processes
• lack of global time frame
• nondeterminism

Communication in distributed system

Main paradigms:

• message passing
• shared memory

Asynchronous communication: sending and receiving are independent events (synchronous is the opposite)

Communication protocol detects and corrects errors during message passing

Assumptions we make:

• strongly connected network (every node/process can reach any other node)
• each process knows only its neighbors (only local knowledge)
• message passing for communication
• asynchronous communication
• channels can be non-FIFO (messages can overtake each other)
• channels don’t lose, duplicate, or mess up messages
• delay of messages in channels is arbitrary, but not infinite
• stable network and processes don’t crash
• processes have unique IDs

Directed vs bidirectional channels

• directed: one way
• bidirectional: messages can go both ways

complexity measures:

• message complexity: total num messages exchanged
• bit complexity: total num bits exchanged
• time complexity: amount of time consumed (assume even processing takes no time, message received max one time unit after it’s sent)
• space complexity: amount of memory needed for the processes
• we consider worst- and average-case complexity

Big O notation

• complexity measures show how resource consumption grows in relation to input size
• an algorithm with worst-case message complexity (n²) for input size n takes max in order of n² messages
• “in the order of”: give or take some constant
• f = O(g) if for some C > 0, f(n) ≤ C·g(n) for all n ∈ ℕ
• f = Θ(g) if f = O(g) and g = O(f) (both upper and lower bound)

Transition systems

• global state of distributed system is a “configuration”
• configuration evolves in discrete steps called “transitions”
• transition system:
  • set C of configurations
  • binary transition relation → on C
  • and set I ⊆ C of initial configurations
• A state is terminal if there are no transitions from it

Execution: sequence γ₀ γ₁ γ₂… of configurations that

• either is infinite,
• or ends in terminal configuration such that
  • γ₀ ∈ L and
  • γⱼ → γⱼ₊₁ for j = 0,1,2,…
• configuration is reachable if there is a sequence of transitions from an initial state to it

States and events

• configuration of distributed system: states at its processes & messages in its channels
• transition associated to event (or two events if synchronous) at one (or two) of its processes
• events: internal, send, receive
• initiator process: if its first even is internal or send
  • algorithm is centralised if only one initiator
  • decentralized if more than one

Assertion:

• predicate on configurations of an algorithm
• safety property is always true in each configuration (“something bad will never happen”)
• liveness property is true in some configuration of each execution (“something good will eventually happen”)

Invariants:

• assertion P on configurations is invariant if:
  • holds for all initial states
  • if holds in states on both sides of transitions
• each invariant is a safety property

Causal order

• in configuration of async system, applicable events at different processes are independent
• causal order (≺ symbol) on occurrences of evens in execution is smallest transitive relation st
  • in english, if a happens before b, then a ≺ b
  • full definition:
    • if events a,b at same process, and a occurs before b, then a ≺ b
    • if a send and b corresponding receive, then a ≺ b
  • irreflexive! (you clearly can’t have a before b and b before a)

Computations

• if neither a ⪯ b nor b ⪯ a, then a and b are concurrent
• permutation of concurrent events in execution doesn’t affect result of execution
• these permutations form a computation

Clocks

Lamport’s clock

• logical clock C maps occurrences of events in computation to a partially ordered set, such that a ≺ b ⇒ C(a) < C(b)
• Lamport’s clock LC assigns to each event a the length of k of longest causality chain a₁ ≺ … ≺ aₓ = a
• LC can be computed at runtime:
  • one list of clock values per process, length of the list is same as number of messages
  • each message increases the clock value by 1
  • on a receive, wait until the corresponding send is done, and then the receive has the incremented clock value

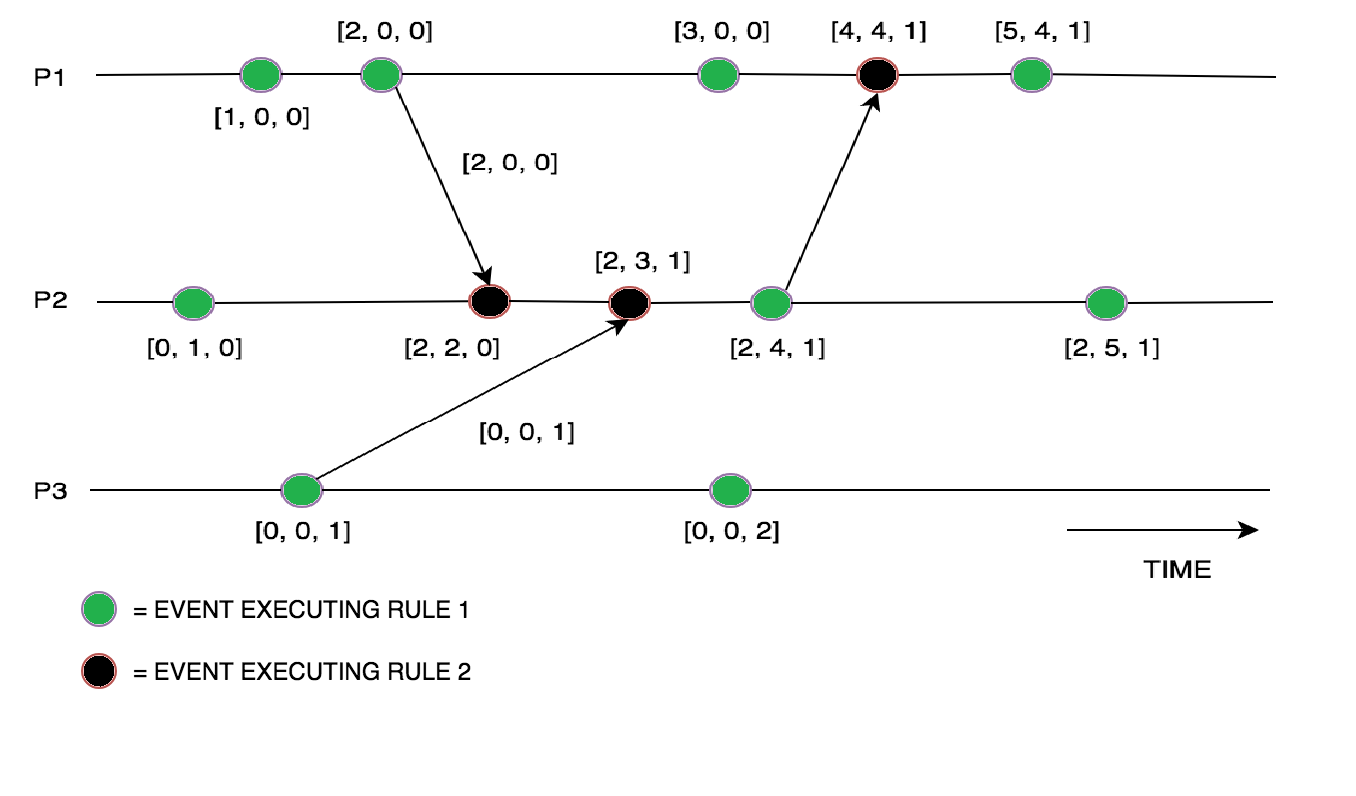
Vector clock

• given processes p₀…pₓ₋₁
• each process has a list of vectors (k₀..kₓ₋₁) that are clock values corresponding to processes (e.g. k₀ is first process, k₁ is second process, etc.)
• a message increments the process’ clock value by 1
• a receive message also takes the maximum of the other clock values in the process’ vector and the values in the vector of the process with the corresponding send message

Snapshots

snapshot of execution of distributed algorithm should return configuration of execution in the same computation

distinguish: basic messages of underlying distributed algorithm, control messages of snapshot algorithm

snapshot of basic execution contains

• local snapshot of basic state of each process
• channel state of basic messages in transit for each channel

meaningful snapshot: if configuration of execution in same computation as actual execution

• for each message m, sender, p, receiver q, must agree whether m is pre- or post-snapshot

Chandy-Lamport algorithm

decentralised. assumes directed network with FIFO channels.

1. Some node takes a snapshot, starts recording on channels, then sends out marker messages across all channels before any other mesages
2. When a node receives the marker control message:
   • if this is the first one it received:
     • take a snapshot (record its own state)
     • mark the corresponding channel as empty
     • start recording on all other channels
     • send out marker messages on all channels, before any other messages
   • else:
     • stop recording the corresponding channel
     • set that channel’s state to all messages received since the snapshot

This is a very good explanation

Complexity:

• message: Θ(E) (with E number of channels)
• worst-case time: (D) (with D the diameter)

Lai-Yang algorithm

allows that channels are non-FIFO

• initiators take local snapshot of their state
• when process takes local snapshot, appends ‘true’ to each outgoing basic message
• if process that hasn’t yet taken snapshot receives message with ‘true’, or control message, for the first time, it takes local snapshot before reception of the message
• channel state is basic messages without ‘true’ that receives after its local snapshot
• processes count how many basic messages without ‘true’ they sent/received for each channel
• when p takes a snapshot, p sends a control message to q, telling q how many basic messages without ‘true’ were sent to pq
• for multiple snapshots, each snapshot has sequence number and basic message carries sequence number of last snapshot at sender instead of ‘true’