Lambda terms

abstraction

𝜆.M is function mapping of x to M 𝜆x.square x is function mapping of x to square x

application

F M is application of function F to argument M

terms as trees

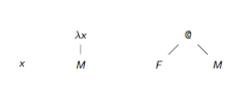
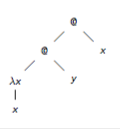
parentheses

application is associative to the left (M N P) —> ((M N) P)

outermost parentheses are omitted M N P —> (M N P)

lambda extends to the right as far as possible 𝜆x.M N —> 𝜆x.(M N)

combining lambdas is possible 𝜆xy.M —> 𝜆x.𝜆y.M

start with most nested lambda (𝜆x.𝜆y.M) —> 𝜆x.(𝜆y.M))

currying

reduces function with several arguments to functions with single arguments

f: x => x+x —> 𝜆x.x+x g: (x,y) => x+y —> 𝜆x.𝜆y.x+y

free/bound variables

x is bound by the first 𝜆x above it in the term tree (underlined)

• 𝜆x.x
• 𝜆x.x x
• (𝜆x.x)x
• 𝜆x.y x

variables that aren’t bound are free (such as y in the last example)

substitution

M[x := N] means: result of replacing all free x in M by N

• x[x := N] = N
• a[x := N] = a
• (P Q)[x := N] = (P[x := N]) (Q[x := N])
• (𝜆x.P)[x := N] = 𝜆x.P
• (𝜆y.P)[x := N] = 𝜆y.(P[y := N]) if x ≠ y

alpha conversion

renaming bound variables (in case of possible name clashes)

• 𝜆x.x = 𝜆y.y
• (𝜆x.y)[y := x] = 𝜆z.x

P = αQ only if Q can be obtained from P by finitely many changes of bound variables in context

beta-reduction (dynamic):

(𝜆x.x)y —> By (𝜆x.x)y —> By (𝜆x.xz)y —> Byz (𝜆x.z)y —> Bz

In general: (𝜆x.M)N —> BM[x := N]