Intelligent Systems

Table of Contents

Logical agents

What is logic

logic: generic method to deal with partial/imperfect/implicit information

we need:

knowledge-based/logical agents must be able to:

online/exploratory search: go to position, evaluate all options, possibly look ahead. have to re-evaluate current position.

Syntax

Propositional logic (PL)

assumes world contains facts

uses proposition symbols to state these facts.

pros:

cons:

First order logic (FOL)

an extension of propositional logic.

allows variables to range over atomic symbols in the domain.

assumes world contains:

Basic elements:

Sentences

Atomic sentence = predicate (term_1,..., term_n)
                  or term_1 = term_2
Term = function(term_1,..., term_n)
      or constant
      or variable

Complex sentences are made from atomic sentences using connectives.

Quantification

Universal quantification

∀

∀x P is true in a model m iff P is true with x being each possible object in the model

(you can roughly translate that to conjunctions)

typically used with ⇒

CARE: ∀x ∀y ≠ ∀y ∀x

Existential quantification

∃

∃x P is true in a model m iff P is true with x being some possible object in the model

(you can roughly translate that to disjunction of instantiations of P)

typically used with ∧

watch out, if you use it with ⇒, it works even if the LHS is false!

CARE: ∃x ∃y ≠ ∃y ∃x

Quantifier Duality

each quantifier can be expressed in terms of the other

e.g. these are the same:

Decidability vs undecidability

undecidability

decidability

Knowledge engineering in FOL

  1. Identify the task
  2. Assemble relevant knowledge
  3. Decide on vocabulary of predicates, functions, and constants
  4. Encode general knowledge about the domain (terms that we want to use)
  5. Encode description of the specific problem instance
  6. Pose queries to the inference procedure and get answers

Choice of formalisms

first-order logic: represents knowledge

propositional logic: used for reasoning (“propositionalisation”)

then use reasoner to check for entailment of propositional logic knowledge base an decision query

Propositionalising FOL

Reduction to propositional inference

every FOL KB can be propositionalised so as to preserve entailment

if a sentence α is entailed by an FOL KB, it is entailed by a finite subset of the propositionalised KB

Universal instantiation (UI):

every instantiation of a universally quantified sentence is entailed by it.

Universal instantiation

example:

∀x King(x) ∧ Greedy(x) ⇒ Evil(x)
King(John) ∧ Greedy(John) ⇒ Evil(John)
etc.

Existential instantiation (EI):

Existential instantiation

example:

∃x Crown(x) ∧ OnHead(x,John)
Crown(C_1) ∧ OnHead(C_1, John)

Applying in Schnapsen - Strategies (examples)

Play Jack

check whether card is a jack:

KB |= PlayJack(x) ?

represent strategy:

∀x PlayJack(x) ⇔ Jack(x)

represent game information:

KB = {Jack(4), Jack(0), Jack(14), Jack(19)}
Play cheap

only play Jacks: check whether card is cheap

KB |= PlayCheap(x) ?

represent strategy:

∀x PlayCheap(x) ⇔ Jack(x) ∨ Queen(x) ∨ King(x)

represent game information:

KB = {Jack(4), Jack(9), Jack(14), Jack(19), Queen(5), ...}
Play trump marriage
TrumpMarriage(x) ⇔ Q(x) & Trump(x) & ∃y: SameColor(x,y) & K(y) & MyCard(y)
SameColor(x,y) ⇔ (C(x) & C(y)) ∨ (D(x) & D(y)) ∨ (H(x) & H(y)) ∨ (S(x) & S(y))

Semantics

Interpretations & Models

interpretation: assignment of meaning to symbols of formal language

model: interpretation that satisfies defining axioms of knowledge base

m is a model of a sentence α if α holds in m.

M(a) is the set of all models of a.

each model specifies true/false for each proposition symbol (∧, ∨, ¬, ⇒, ⇐, ⇔)

Entailment

the knowledge base (KB) entails α: α follows from the information in the knowledge base (KB |= α)

KB entails α iff α holds in all worlds where KB is true.

a knowledge base is the rules + observations.

a sentence is:

two statements are logically equivalent if they are true in same set of models:

α ≡ β iff α |= β and β |= α

Truth

sentences are true with respect to model and interpretation.

model contains objects and relations among them

interpretation specifies referents for:

an atomic sentence $predicate(term_1, …, term_n)$ is true iff the objects referred to by $term_1,…, term_n$ are in the relation referred to by $predicate$

Validity

valid if it is true in all models.

e.g. True, A ∨ ¬A, A ⇒ A, (A ∧ (A e.g. True, A ∨ ⇒ B)) ⇒ B)

Satisfiability

Calculus (algorithms for inference)

Properties of inference

sound: if an algorithm $|-$ only derives entailed sentences. i.e. if KB $|-$ α also KB |= α

complete: if an algorithm derives any sentence that is entailed. i.e. KB |= α implies KB |- α

a calculus terminates if it finds entailed sentences in finite time.

a logic is decidable if there is sound and complete calculus that terminates.

Proof methods

  1. Model checking and search
  1. application of inference rules
Truth Tables for inference

enumerate interpretations and check that where KB is true, α is true.

$fact_1$$fact_2$$fact_3$$KB$$α$
falsefalsefalsefalsetrue
falsefalsefalsefalsetrue
falsetruefalsetruetrue

algorithm:

for (m in truth assignments) {
  if (m makes F true) return "satisfiable"
}
return "unsatisfiable"
Effective proofs by model checking

Clever search (depth first, redundancy, heuristics)

Two families of efficient algorithms for propositional inference based on model checking

Clause Normal Form (CNF)

memo technique: the C in CNF for conjunction normal form

A PL formula is in CNF if it is a conjunction of disjunctions of literals.

calculating CNF:

  1. Remove implications:
  1. Move negations inward:
  1. Move conjunctions outward:
  1. Split up conjunctive clauses:
DPLL algorithm

when you have CNF, you can run the DPLL algorithm. determines if propositional logic sentence in CNF is satisfiable.

returns true if F is satisfiable, false otherwise.

basically assign values until contradiction, then backtrack.

Improving DPLL:

the algorithm:

dpll (F, literal) {
  remove clauses containing literal
  shorten clauses containing ¬literal
  if (F contains no clauses)
    return true
  if (F contains empty clause)
    return false
  if (F contains a unit or pure literal)
    return dpll(F, literal)

  choose P in F
  if (dpll(F, ¬P))
    return true

  return dpll(F, P)
}
Heuristic search in DPLL

used in DPLL to select proposition for branching

idea: identify most constrained variable, likely to create many unit clauses

MOM’s heuristic: most occurrences in clauses of minimum length

why is it better than truth table enumeration?

proving entailment KB |= a by refutation:

  1. translate KB into CNF to get cnf(KB)
  2. translate ~a into CNF to get cnf(~a)
  3. add cnf(~a) to cnf(KB)
  4. apply DPLL until either satisfiable (model is found) or unsatisfiable (search exhausted)
  5. if satisfiable, not entailed. otherwise, entailed.
Satisfiability modulo theory

Boolean satisfiability (SAT): is there an assignment to the $p_1, p_2, …, p_n$ variables such that $\phi$ evaluates to 1?

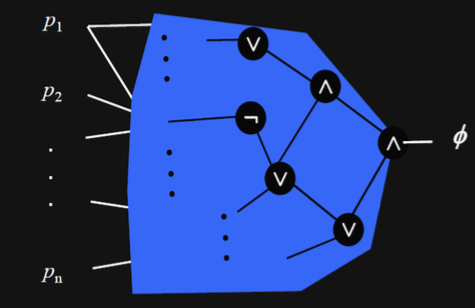
Boolean satisfiability diagram

SAT vs SMT:

SMT theories:

Rule-based reasoning

Inference rules

inference rule: logical form consisting of function taking premises, analyzing their syntax, and returning one or more conclusions

Modens Ponens: $\frac{\alpha\implies\beta,;\alpha}{\beta}$

And-elimination: $\frac{\alpha\land\beta}{\alpha}$

logical equivalences used as rules: $\frac{\alpha\iff\beta}{(\alpha\implies\beta)\land(\beta\implies\alpha)}$

all logical equivalence rewriting rules:

Rewriting rules for logic

Searching for proofs

Finding proofs is like finding solutions to search problems.

monotonicity: set of entailed sentences can only increase as info is added to the knowledge base.

Forward and backward chaining

FC is data-driven, automatic, unconscious:

BC is goal-driven, appropriate for problem-solving

Resolution

a rule is sound if its conclusion is evaluated to true whenever the premise is evaluated to true.

can be shown to be sound using truth table:

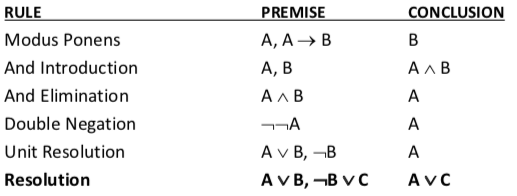
Sound rules for inference

properties resolution:

algorithm (again proof by refutation):

  1. Convert KB ∧ ¬ α into CNF
  2. Apply resolution rule to resulting clauses
  3. Continue until: a) no new clauses can be added, hence α does not entail β b) two clauses resolve to entail empty clause, hence α entails β