Intelligent Systems
Table of Contents
Probability and Uncertainty
one often has to deal with info that is underspecified, incomplete, vague, etc.
logic by itself is not sufficient for these problems.
Vagueness: Fuzzy Set Theory
model theory often based on set theory
fuzzy set theory allows something to be to some degree an element of a set
dominant approach to vagueness (mostly because wtf else can you do)
Fuzzy sets
- universe U, object x ∈ U
- membership function for fuzzy set A is defined to be function $f_A$ from U to [0,1]:
- $f_A(x)=y$: x is a member of A to degree y
- $f_A(x)=1$: x is certainly member of A
- $f_A(x)=0$: x is certainly not a member of A
- ${x | f_A(x)>0}$: support of A
modifiers (hedges)
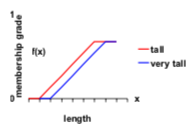
operations on fuzzy sets:
- complement: $f_{\sim{A}}(x)=1-f_A(x)$
- union: $f_{A\cup B}(x)=\max(f_A(x),f_B(x))$
- intersection: $f_{A\cap B}(x)=\min(f_A(x), f_B(x))$
- subset: $A\subset B \iff \forall{x}(f_A(x)\leq f_B(x))$
semantics – multivalued fuzzy logic
- v(¬ A) = 1-v(A)
- v(A ∨ B) = max(v(A), v(B))
- v(A ∧ B) = min(v(A), v(B))
- v(A → B) = min(1, 1 - v(A) + v(B))
Fuzzy relations
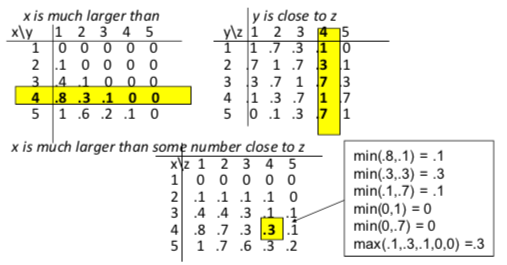
fuzzy sets can denote fuzzy relations between objects. e.g. approximately equal, close to, much larger than, etc.
fuzzy composition:
$f_{R \circ S} (\langle x,z\rangle ) = \max_{y \in Y} \min(f_R (\langle x,y\rangle ), f_S (\langle y,z\rangle ))$
hands-on example:
Evaluation
- good – flexible, coincides with classical set theory, sever successful applications of fuzzy control
- bad – requires many arbitrary choices, tends to blur differences between probabilistic uncertainty/ambiguity/vagueness
Uncertainties: Probability Theory
General
main interpretations of probability theory:
- optivist (frequentist) probability
- frequentism: probability is only property of repeated experiments
- probability of event: limit of relative frequency of occurrence of event, as number of repetitions goes to infinity
- subjective probability
- Bayesianism: probability is an expression of our uncertainty and beliefs
- probability of event: degree of belief of idealized rational individual
sample space Ω: set of single outcomes of experiment
event space E: things that have probability (subsets of sample space). if sample space is finite, event space is usually power set.
Axioms of probability
for any event A, B:
- $0 \leq P(A) \leq 1$
- $P(\Omega) = 1$
- $P(A \cup B) = P(A) + P(B) - P(A \cap B)$
can derive:
- $P({}) = 0$
- $P(\Omega) = 1$
- $\text{if} A \subset B, P(A) \leq P(B)$
conditional probability (“A given B”):
$P(A|B) = \frac{P(A \cap B)}{P(B)}$
Joint probability distributions
for a set of random variables, it gives probability of every atomic even on those random variables.
e.g. P(Toothache, Catch, Cavity):
| toothache | > | ¬ toothache | > | |
|---|---|---|---|---|
| catch | ¬ catch | catch | ¬ catch | |
| cavity | 0.108 | 0.012 | 0.072 | 0.008 |
| ¬ cavity | 0.015 | 0.064 | 0.144 | 0.576 |
inference by enumeration:
- for any proposition Φ, sum atomic events where it’s true – $P(\Phi) = \sum_{\omega : \omega \models \Phi} P(\omega)$
- compute conditional probability by selecting cells – e.g. for P(¬ cavity | toothache), select toothache column and (¬ cavity) cells
use Bayes’ rule for opposite conditionals (like finding P(disease | symptom) from P(symptom | disease))
Bayesian networks
simple graphical notation for
- conditional independence assertions
- compact specification of full joint distributions
syntax:
- set of nodes, one per variable
- directed acyclic graph, with a link meaning “directly influences”
- conditional distribution for each node given its parents – $P(X_i | Parents(X_i))$
topology example:
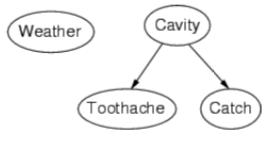
what does it mean?
- weather is independent of other variables
- toothache and catch are conditionally independent given cavity.
Evaluation of probabilities
- good – sound theoretical basis, can be extended to decision-making, some good tools available
- bad – not always computationally easy, need lots of data which may be hard to get