State space search

How do we find the solutions of previous problems?

search the state space
search through explicit tree generation: root is initial state, nodes/leaves generated through successor function
search generates a graph

state: representation of a physical configuration

node: data structure in the search tree. it contains state, parent node, actions, etc.

Uninformed search strategies

strategy defines picking order of node expansion

uninformed methods: only use problem definition

informed methods: use heuristic function to estimate cost of solution

evaluating performance:

does it always find a solution if there is one? (completeness)
does it find least-cost solution? (optimality)
how many nodes generated/expanded? (time complexity)
how many nodes are stored in memory during search? (space complexity)
complexity measured in terms of:
- b: max branching factor of search tree)
- d: depth of least cost solution
- m: max depth of state space, could be infinite
time/space complexity measured in terms of max branching factor of search tree, depth of least cost solution, max depth of state space (could be infinite)

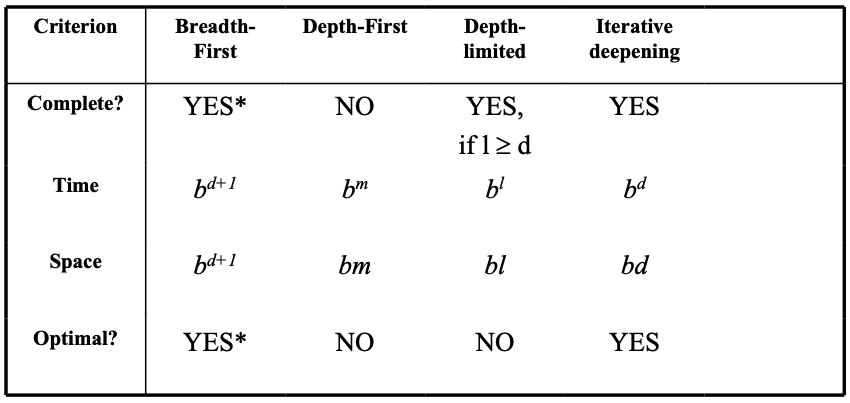
Breadth-first (BF) search

algorithm:
- expand shallowest unexpanded node
- implementation - fringe (nodes that have to be explored) is a FIFO queue
evaluation:
- completeness: yes, if branching factor b is finite
- time complexity: if every state has b successors, and solution is at depth d, then $O(b^{d+1})$ because of number of nodes generated
- space complexity: shitty if every node has to be in memory - $O(b^{d+1})$
- optimality: in general yes, unless actions have different cost
memory requirements are bigger problem than execution time

Depth-first (DF) search

algorithm:
- expand deepest unexpanded node
- implementation: fringe is a stack
evaluation:
- completeness: no, unless search space is finite and no loops are possible
- time complexity: shitty if m is larger than d (depth of optimal solution) – $O(b^m)$. but if many solutions, faster than BF
- space complexity: backtracking search uses less memory, one successor instead of all b – $O(bm+1)$
- optimality: no, same issues as completeness

Depth-limited search

DF-search with depth limit l (nodes at depth l have no successors)
solves infinite-path problem
evaluation:
- time: $O(b^l)$
- space: $O(bl)$
- completeness: not if l < d
- optimality: not if if l > d

Iterative deepening search

strategy to find best depth limit l
often used in combination with DF search
after each iteration, throw away everything and increase depth limit
combines benefits of DF (space complexity) and BF search (time complexity)
evaluation:
- completeness: yes (no infinite paths)
- time: $O(b^d)$
- space: $O(bd)$

Informed search (heuristics)

Heuristic function: “educated guess that reduces/limits search for solutions”

informedness property of heuristics:

two heuristics $h_1(n),; h_2(n)$ with $0 \leq h_1(n) \leq h_2(n) \leq h*(n)$
then $h_2(n)$ is more informed than $h_1(n)$
with $h_1$ fewer nodes have to be searched with $h_2$
but $h_2$ is often more expensive to calculate
perfect heuristics: $h(n) = h*(n)$
trivial heuristics: $h(n) = 0$

Best-first search

the general approach of informed search
node selected for expansion based on evaluation function f(n)
evaluation function measures distance to goal, choose node which appears best
fringe is queue in order of decreasing desirability

A Search

best-known form of best-first search

avoid expanding paths that are already expensive

evaluation function: $f(n) = g(n) + h(n)$

g(n) the cost so far to reach node n
h(n) estimated cost to get from node n to goal
f(n) estimated total cost of path through node n to goal

A* Search

A search, but with an admissible heuristic

heuristic is admissible if it never overestimates the cost to get to goal
admissible heuristics are optimistic
formally: $h(n) \leq h*(n)$ where $h*(n)$ is true cost from n to goal

evaluation:

complete: yes
time: exponential with path length
space: all nodes are stored
optimal: yes

Adversarial search

search has no adversary, solution is a (heuristic) method for finding a goal

games have an adversary, solution is a strategy. time limits force an approximate solution.

you need a function to evaluate the “goodness” of a game position

types of games:

	deterministic	chance
perfect information	chess, checkers, go, othello	backgammon, monopoly
imperfect information		bridge poker, scrabble, nuclear war

Minimax

Setup

two players: MAX, MIN

MAX moves first, take turns until game is over. winner gets award, loser gets penalty.

how does this relate to search?

initial state: game configuration e.g. with chess
successor function: list of <move, state> pairs with legal moves
terminal test: game finished?
utility function: numerical value of terminal states (win +1, lose -1, draw 0)
MAX uses search tree to determine next move

Optimal strategies

find contingent strategy for MAX assuming infallible MIN.

assume that both players play optimally.

given game tree, optimal strategy can be found with minimax value of each node:

    minimax(n) = utility(n)                      if n is a terminal
                 minimax(max(successors of n))   if n is a max node
                 minimax(min(successors of n))   if n is a min node

Evaluation

complete: yes
time: $O(b^m)$
space: $O(bm)$
optimal: yes

Reducing problems of complexity with Minimax

Cutting off search:

instead of if TERMINAL(state) then return UTILITY(state) do if CUTOFF-TEST(state, depth) then return EVAL(state)

this introduces fixed-limit depth. also loses completeness!

utility: value based on quality of state

heuristics: value based on estimation of quality of state

heuristic EVAL:

produces estimate of expected utility of a game from a given position
should order terminal nodes in same way as utility
computation shouldn’t take too long

Alpha-Beta pruning (efficient Minimax)

with minimax, the number of states is exponential to number of moves

so, don’t examine every node and prune the subtrees you don’t have to examine

Alpha: value of best MAX choice so far

Beta: value of best MIN choice so far

you prune the rest of the level if, at any point, beta <= alpha.

pruning doesn’t affect final results, entire subtrees can be pruned

good move ordering improves effectiveness of pruning

with ‘perfect ordering’, time complexity is: $O(b^{m/2})$

Search with no or partial information

problems:

contingency: percepts provide new info
exploration: when states/actions of environment are unknown
sensorless/conformant: agent may have no idea where it is

Perfect information Monte Carlo sampling (rdeep)

rollout:
- assume a belief state (with perfect info)
- play random game in that state.
average the rollouts
choose one with max average

Games with chance

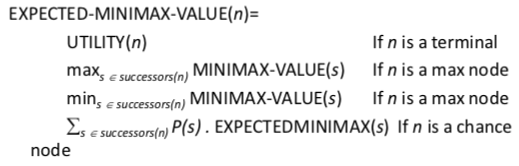
Summary (Schnapsen)

Phase 2: minimax & alpha-beta pruning

Phase 1: PIMC sampling

what next? give the agent information about the game

Search direction

Data-driven: start with initial state (e.g. a maze)

Goal-driven: start with goal state, but has bigger branching factor (TODO confirm this)

Intelligent Systems

Table of Contents