Definability and Undefinability results

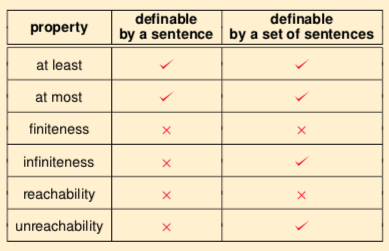
expressible frame properties in predicate/modal logic:

for model cardinality

model cardinality:

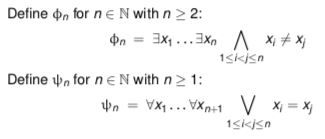
for all models M and all n ≥ 2 it holds that:

• M ⊨ Φn ⇔ A has at least n elements
• M ⊨ ψn ⇔ A has at most n elements
• M ⊨ Φn ∧ ψn ⇔ A has precisely n elements

model infiniteness is definable by a set of formulas Δ:

• M ⊨ Δ ⇔ M has an infinite domain

model finiteness is undefinable (single formula):

• there’s no sentence ψ such that
• all M: M ⊨ ψ ⇔ M has a finite domain

model finiteness is undefinable (set of formulas):

• there’s no set of formulas Γ such that
• all M: M ⊨ Γ ⇔ M has a finite domain

mode infiniteness is undefinable (single formula)

• there’s no sentence ψ such that
• all M: M ⊨ ψ ⇔ M has infinite domain

for reachability

“v is reachable via R from u”. thinking of R as arrows, it means that there’s a path from v to u.

search for formulas χn that express reachability in n steps:

Reachable in n steps:

1. u = v
2. R(u,v)
3. ∃x₁ (RU, x₁) ∧ R(x₁, v))
4. ∃x₁ ∃x₂ (R(u, x₁) ∧ R(x₁, x₂) ∧ R(x₂, v))
5. ….

shorthand: χ₂(c,d) denotes formula ∃x₁ (R(c, x₁) ∧ R(x₁, d))

reachability is undefinable:

Let R be a binary relation symbol.

1. In predicate logic, reachability by R-steps is

• not definable by a sentence
• not definable by a set of sentences

2. In predicate logic, unreachability by R-steps is

• not definable by a single sentence
• definable by a set of sentences

General overview