Modal logic

modal logic allows reasoning about dynamics – futures, knowledge, beliefs, etc.

modalities (unary connectives):

• □ (box): sure, always, has to be, knows, guaranteed (kinda like ∀)
• ◇ (diamond): possibly, sometimes, maybe, believes is possible, possible result (kinda like ∃)

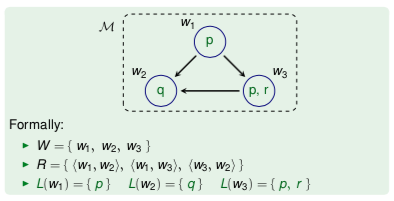
Kripke model M = (W, R, L) consists of:

• W worlds
• R accessibility relation
• L labeling function: which propositional letters are true in which world (w ⊩ p ↔ p ∈ L(w))

Kripke models define truth per world.

Truth in worlds

M, w ⊩ Φ means formula Φ is true in world w of Kripke model M.

◇ Φ is true in world w if there exists a world w’ such that R(w, w’) and Φ is true in w’.

□ Φ is true in world w if Φ is true in all worlds w’ with R(w, w’). special case when world has no outgoing edge, ◇ Φ never holds and □ Φ always holds.

Truth in Kripke models

Φ is true in Kripke model M = (W, R, L) (i.e. M ⊨ Φ), iff x ⊩ Φ for every world x ∈ W.

all propositional tautologies also hold in modal logic.

Semantic implication/entailment

M,w ⊨ ψ in every world w in every Kripke model where M,w ⊨ Φ₁, …, M,w ⊨ Φn.

modal validity: ⊨ ψ if in every world w in ever Kripke model M holds M,w ⊨ ψ.

modal logical equivalence: Φ ≡ ψ if M,w ⊨ Φ ↔ M,w ⊨ ψ. in other words, Φ ≡ ψ ↔ Φ ⊨ ψ and ψ ⊨ Φ.

Frames

frame: Kripke model without labeling. F = (W,R), W worlds, R accessibility relation

Φ is valid in frame F (i.e. F ⊨ Φ) if for every labeling L, Kripke model M = (W,R,L) makes Φ true.

Correspondence of formulas and frame properties

• reflexive:
  • F ⊨ □ p → p
  • F ⊨ p → ◇ p
• symmetric:
  • F ⊨ q → □ ◇ q
  • F ⊨ ◇ □ p → p
• transitive:
  • F ⊨ □ p → □ □ p
  • F ⊨ ◇ ◇ p → ◇ p
• serial:
  • F ⊨ ◇ T
  • F ⊨ □ p → ◇ p
• functional: □ p ↔ ◇ p