Sets

Recap from logic and sets:

• empty set Ø = {x | false}
• universal set U = {x | true}
• union A ∪ B = {x | x ∈ A or x ∈ B}
• intersection A ∩ B = {x | x ∈ A and x ∈ B}
• complement Ā = {x | x ∉ A}
• difference A \ B = {x | x ∈ A and x ∉ B}

Theorems:

• A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
• (A \ B) \ C = A \ (B ∪ C)

Relations

definitions of properties:

• reflexive: ∀x R(x,x)
• symmetric: ∀x ∀y (R(x,y) → R(y,x))
• transitive: ∀x ∀y ∀z ((R(x,y) ∧ R(y,z)) → R(x,z))
• serial: ∀x ∃y R(x,y)
• functional: ∀x ∃y (R(x,y) ∧ ∀z (R(x,z) → z=y))

Order types

partial order:

• reflexive
• transitive
• antisymmetric

total order:

• partial order
• ∀ a,b (R(a,b) ∨ R(b,a))

strict partial order: partial order but irreflexive

strict total order:

• strict partial order
• ∀ a,b (R(a,b) ∨ (a=b) ∨ R(b,a))

equivalence relation:

• reflexive (∀a, a ≡ A)
• symmetric
• transitive

Natural numbers & induction

Set of natural numbers is N ∈ (0,∞)

Principle of induction: let P be a property of natural numbers. Suppose P holds for zero, and whenever P holds for a natural number n, then it holds for its successor n+1. Then P holds for every natural number.

As a natural deduction rule:

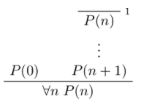
Recursive definitions

Let A be any set, suppose a is in A, and g: N × A → A. Then there is a unique function f satisfying:

• f(0) = a
• f(n+1) = g(n, f(n))

Typically to prove something about a recursively defined function is to use induction.