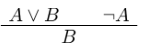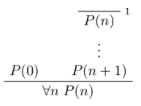Backward proofs

This is like going up the proof tree.

Tactical propositions look like this:

lemma lemma_name :
    statement :=
begin
    proof
end

It can also be a one-line proof, with by:

lemma lemma_name :
    statement :=
by tactic

Tactics:

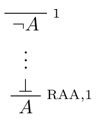
intro h creates assumption h from left-hand of implication or quantifiers (intros for multiple at once)
apply h matches goal’s conclusion with conclusion of h and adds h’s hypotheses as new goals
exact h matches goal’s conclusion with conclusion of h, closing the goal (could also use apply)
assumption finds a hypothesis from the context that matches the goal’s conclusion and applies it
refl proves reflexivity (l = r) including unfolding definitions, β reduction, and more
and.intro, and.elim_right, and.elim_left, or.intro_right, or.intro_left, or.elim are for logical connectives (∧, ∨)
eq.refl for reflexivity, eq.subst h to substitute h into equality
rw h applies h once as left-to-right rewrite rule. can apply right-to-left by writing ←h.
not_def: ¬a ↔ a → false
simp [h1, h2...] applies rewrite rules and hypothesis set
cc applies congruence closure
em applies Law of Excluded Middle (p ∨ ¬p)
induction' performs proof by induction, yields one subgoal per constructor
rename h1 h2 renames h1 to h2
clear h1 removes h1