Partial orders

partial order on V: relation R of type V × V. satisfies reflexivity, anti-symmetry, transitivity

example: relation ≤ is partial order on N

• ∀n: n ≤ n (reflexivity)
• ∀m, n: m≤n ∧ n≤m ➝ m = n (anti-symmetry)
• ∀k, m, n: k≤m ∧ m≤n ➝ k≤n (transitivity)

example: the relation ⊆ is partial order on P(V)

• ∀A: A ⊆ A (reflexivity)
• ∀A,B: A ⊆ B ∧ A ➝ A = B (anti-symmetry)
• ∀A,B,C: A ⊆ B ∧ B ⊆ C ➝ A ⊆ C (transitivity)

linear ordering relations

partial order R on set V, then:

• x, y ∈ V are comparable if x R y or y R x
• R is linear/total order if all x,y ∈ V are comparable

e.g. relation ≤ on N: for all n,m in N — n ≤ m or m ≤ n — total

e.g. relation ⊆ on P({1,2}): {1} is not a subset of {2}, {2} is not a subset of {1} — not total

strict partial ordering relations

if partial order R on set V, then strict partial order S corresponding to R is defined by

x S y ⟷ x R y and x ≠ y

a strict partial order is irreflexive, anti-symmetric, transitive

Hasse diagrams

apparently a partial ordering relation is complicated as fuck:

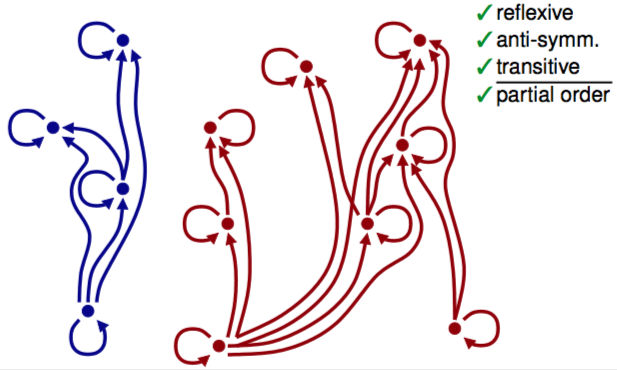
so get rid of some arrows and make a Hasse diagram — omit reflexivity and transitivity

the arrows create chains that split and merge, elements in the same chain are comparable

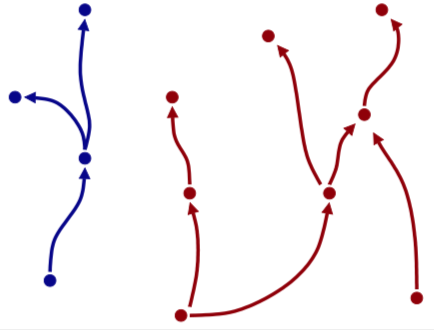
Algorithm:

1. For all x ∈ V — Gx := {y : y ≠ x and x R y}
2. For all x ∈ V — Hx := Gx \ {z : z ∈ Gy for a y ∈ Gx}
3. For all x ∈ V — draw and arrow from x to every y ∈ Hx

example:

Cartesian order on A × B

<a1, b1> ≤ <a2, b2> ⟷ a1 ≤A a2 and b1 ≤B b2

ordered by points, if both are smaller

cartesian order on A × B is a partial order

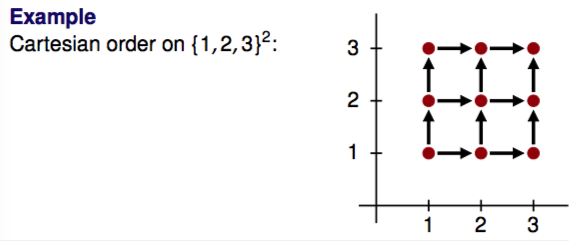
Lexicographic order on A × B

<a1, b1> ≤ <a2, b2> ⟷ (a1 <A a2) ∨ (a1 = a2 ∧ b1 ≤B b2)

like in a dictionary

lexicographic order on A× B is a partial order, total if ≤A on A and ≤B on B are total

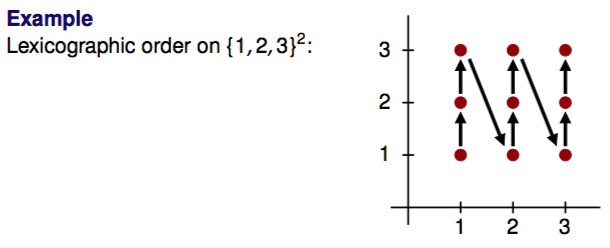
Minimal and maximal elements

(V, ≤) is a partially ordered set, A ⊆ V, m ∈ A

m is:

• largest element of A — if ∀a ∈ A : a ≤ m
• smallest element of A — if ∀a ∈ A : m ≤ a
• maximal element of A — if ∀a ∈ A : (M ≤ a ➝ m = a) — no outgoing arrows on Hasse diagram
• minimal element of A — if ∀a ∈ A : (a ≤ m ➝ a = m) — no incoming arrows on Hasse diagram

Every maximum of A is a maximal element of A. If A has a maximum, it is the only maximal element.