Predicate Logic

Atomic formulas

role of propositional vars p,q,r is taken over by atomic formulas with objects and predicates

C(j)

• C is a unary predicate symbol
• can mean e.g. Jane (j) is clever (C)

K(a,b)

• K is a binary predicate symbol
• can mean e.g. A knows B
• A and B are objects a and b

Quantifiers

∃x C(x) — somebody is clever

∀x C(x) — everybody is clever

same priority level as for ¬

Models

if L(r,j) means Robert loves Jane, it holds in M1 but not M2

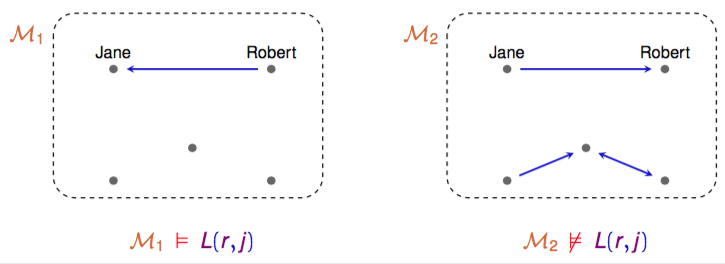
meaning/truth value of a formula from predicate logic depends on underlying model M, consisting of:

• set A of elements
• interpretation of constants (r, j)
• interpretation of predicate symbols (L, C, K)

∀x ϕ is true in M if true for every element in A

∃x ϕ is true in M if true for some element in A

for each e ∈ A, ϕ [x := e] is true in M

Semantic entailment

for formula ϕ, M ⊨ ϕ means that ϕ is true in M

• tautology — true in all models
• contradiction — false in all models
• contingent — true in some model, false in another
• satisfiable — true in some model

Semantic equivalence

1. if for all models M, M ⊨ ϕ ⟷ M ⊨ Ψ
2. then ϕ ≡ Ψ

also, given that “nobody is perfect”, this holds:

¬∃x P(x) ≡ ∀x ¬P(x)

Alpha conversion

you can rename bound variables like in lambda calc

∀x C(x) ≡ ∀y C(y)