Communities

Sociogram: graph-like representation of social structure calculate stats like eccentricity, closeness, betweenness centrality

proximity prestige

• D is digraph with n vertices
• influence domain R-(v) of v is set of vertices from which v can be reached
• proximity prestige: (fraction of vertices that can reach v) / (average distance of those vertices to v)

ranked prestige

• A is adjacency matrix for digraph
• A[v,u] means how much v is appreciated by u

$\sum_{v \neq u} A[v, u] = 1$ for each vertex u

$p_{rank} (v) = \sum_{u \neq v} A[v, u] \times p_{rank} (u)$

$\sum_{v} p_{rank} (v)^2 = 1$

example:

structural balance

• a signed graph (edges labelled +/-) is balanced if all its cycles are positive (product of edge labels is positive)
• if the graph has no cycles, it is balanced
• signed graph is balanced iff its vertices can be partitioned into two disjoint subsets such that:
  • each negative edge joins the subsets, and
  • each positive edge joins vertices in the same subset

affiliation networks

• people are tied together through membership relations
• social structures consist of actors and events
• naturally bipartite, with two sets (Va actors, Ve events)
• represented with an actor-event matrix:

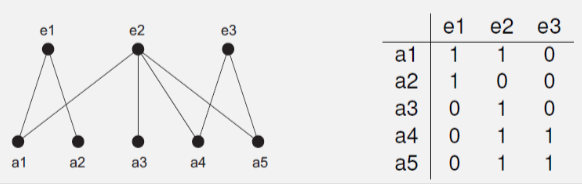
• number of events in which a and b participated

  $NE[a, b] = \sum_{e \in V_e} AE[a, e] \times AE[b, e]$

• number of actors participating in events e and f

  $NA [e, f] = \sum_{a \in V_a} AE[a, e] \times AE[a, f]$