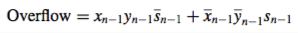Addition/subtraction logic unit

Adders

A half adder takes two inputs, produces sum and carry-out.

A full adder also takes a carry-in.

You can easily get this from a truth table:

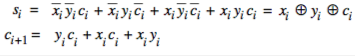
You can make a circuit out of this. Inputs are x, y, and carry. Carry out is $c_{i+1}$:

Sum	Carry

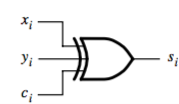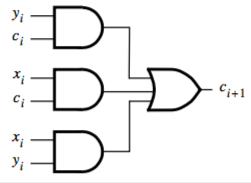That’s represented by the symbol:

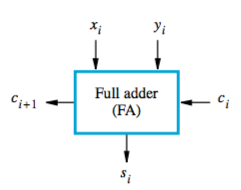
If you want to add n bits, you stick a bunch of them together and make an n-bit ripple-carry adder. $x_{n-1}$ and $y_{n-1}$ are the sign bits:

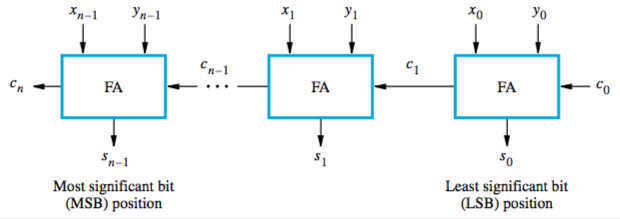
Detecting overflow

Remember that the final carry out is not a part of the result. It’s an overflow when:

• the sign of the sum is different from the sign of the summands
• or the carry-out bits are different

Two logical expressions for detecting overflow (either works):